La tangente è un’altra funzione goniometrica.
Un po’ come seno e coseno, ma anche un po’ diversa.

La tangente è legatissima al seno ed al coseno.
Ma, se loro due servono per risolvere i triangoli, la tangente mi aiuta un po’ di più a capire qualcosa di concreto, almeno per chi lavora nel campo della misura.
La tangente dice qual è la pendenza di un qualcosa…

Scritto così è piuttosto semplicistico e riduttivo.
Ed anche poco corretto
Anche la tangente aiuta a risolvere i triangoli e fa molto di più di dirmi solo la pendenza, ma sai che sto cercando una via semplice per parlare di queste cose e, almeno all’inizio dell’articolo, provo a rimanere fedele alla linea.

In ogni caso, anche per la tangente si parla di tangente di un angolo.

TGα = SENα/COSα

Quella del titolo qui sopra è la definizione di tangente.
È il rapporto tra il seno ed il coseno dello stesso angolo.
Ecco perchè il legame tra loro è forte.

tgα = senα / cosα

Prima di andare avanti ti dico due cose sulla tangente:

è un numero puro (lo erano già seno e coseno e non può che esserlo anche il loro rapporto);
non esiste sempre (?!?! – te lo spiego dopo).

Se guardo al cerchio goniometrico qui sotto ed uso i segmenti, con le loro lettere, posso scrivere che:

tgα = BC / OC

Così come il seno ed il coseno sono individuabili visivamente (perchè sono le due coordinate, X e Y, del punto B), anche la tangente ha la sua visibilità.
Bisogna tracciare un paio di linee in più ma si trova .

Dal punto A, origine degli angoli orientati, disegno la retta tangente al cerchio goniometrico.

… … …

Immagino la tua perplessità.
Retta tangente e tangente di angoli…

Sono la stessa cosa?
No, sono due cose diverse.

Ma sulla perplessità ti do ragione.
Tutto ‘sto rigore e ‘sta precisione della matematica, della geometria e della trigonometria e poi scopri che ci sono due cose che si chiamano nello stesso modo ma hanno significati diversi?

È così, ma è un caso isolato.

La retta tangente viene dalla geometria pura e si riferisce ad una retta che tocca in un solo punto una curva, senza tagliarla (altrimenti sarebbe secante).

La tangente di questo articolo invece è una roba tutta trigonometrica.

Ritorno al cerchio goniometrico.
Dopo aver disegnato la retta tangente in A (e ce n’è solo una che, per altro, è anche perpendicolare al segmento OA), prolungo il segmento OB al di fuori del cerchio.
B è un punto della circonferenza e forma l’angolo al centro α (misurato a partire dal lato OA)

Le due rette si incontrano nel punto T.
Ed ecco la tangente!
La lunghezza del segmento AT è la tangente dell’angolo α.
Oppure, la tangente dell’angolo α è l’ascissa del punto T.

DOMANDE E RISPOSTE SULLA TANGENTE

“Dall’immagine che hai messo qui sopra sembra che la tangente sia maggiore del seno e del coseno. È così?”
Ni…
È sicuramente maggiore di almeno uno dei due…
Seno e coseno possono prendere valori compresi tra -1 e 1.
Per la maggior parte degli angoli sono uno “zero virgola qualcosa“.
E dividere un numero per un altro minore di 1 dà sempre come risultato un valore maggiore di quello di partenza.
Ok questa non è una grande spiegazione ma un po’ funziona…

“Ci sono angoli per cui seno, coseno e tangente sono uguali?”
No.
Se per un angolo di 45° e 225° (e per tutti gli angoli che rispondono alla formula 45°+180°) seno e coseno sono uguali e danno, rispettivamente 0.71 e -0.71, non c’è un angolo che dia lo stesso risultato per la tangente.
L’angolo, la cui tangente fa 0.71 è poco più di 35°.

“Perchè hai scritto che la tangente non esiste sempre?”
Perchè ci sono due casi dove trovare un numero finito, anche se decimale, per la tangente è impossibile.
Qui entra in gioco l’aritmetica pura e la divisione per 0.

Si può dividere un numero per 0?
Ni…
Alle scuole elementari ti insegnano che non si può.
Andando un po’ più avanti ed entrando nei meandri dell’aritmetica più avanzata scopri che il risultato di qualsiasi numero diviso per 0 è un numero grandissimo (nel suo valore assoluto, ossia senza considerare il segno), incalcolabile ed inarrivabile: infnito – ∞

Anche qui ho semplificato molto.
L’impossibilità di dividere un numero per 0 è reale e deriva dalla proprietà della moltiplicazione per 0, ma se entro qui dentro ne esco dopo qualche altro migliaio di parole.

Ci sono due angoli per cui il coseno è 0.
Sono 90° e 270°.

tg90° = sen90° / cos90°
tg90° = 1 / 0 = ∞

tg270° = sen270°/cos270°
tg270° = -1 / 0 = -∞

Si può dire quindi che la tangente esiste per ogni angolo?
No, perchè ce ne sono due (90° e 270°) per cui non se ne risce a dare un valore finito.
In realtà ci sono più di due angoli che incasinano la tangente e sono tutti quelli che si ottengono aggiungendo, in serie, 180° all’angolo retto: 90°, 270°, 450°, 630°, 810°, …
Ma mi fermo al primo giro nel cerchio goniometrico.

Se ritorni al punto T che ti ho mostrato poco prima vedrai che, a mano a mano che il punto B si avvicina all’intersezione della circonferenza con l’asse X (dove c’è la bandierina dei 90°) T è sempre più lontano da A fino a che non riesce più a toccare la tangente geometrica per A e questo succede proprio quando l’angolo al centro è 90°.
Quindi in questo caso il segmento che descrive graficamente la tangente ha un inizio ma non una fine.
È infinito!

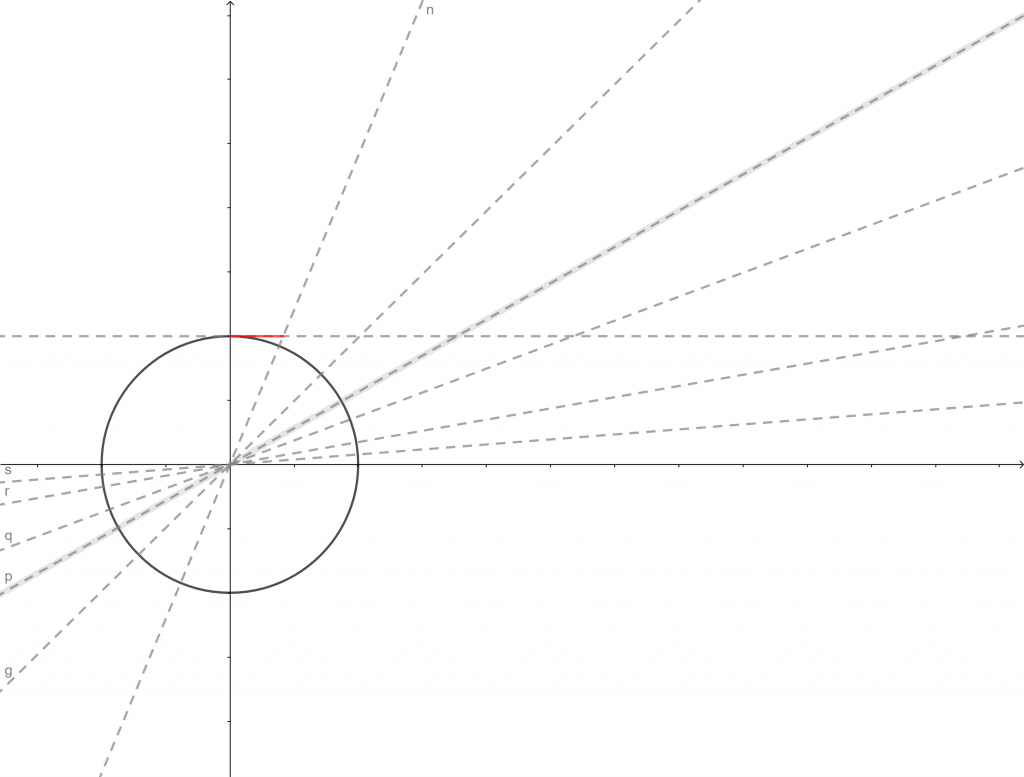
La stessa cosa vale, col segno inverso, nel quadrante opposto, il terzo, andando verso i 270°.

ANGOLI FACILI E PERIODICITÀ DELLA FUNZIONE TANGENTE

Ti metto qui sotto una tabella con i valori di seno, coseno e tangente per una serie di angoli (la seconda colonna riporta il valore dell’angolo in radianti).
In giallo ti ho evidenziato i valori uguali di seno e coseno.
In celeste ci sono le celle dove il valore della tangente è +∞ e -∞.

Non è immediato capirlo dai numeri che ci sono qui sopra ma anche per la tangente ci sono angoli per cui il suo valore è più facile da ricordare di altri.
Eccoli:

tg0° = 0
tg30° = 1 / √3
tg45° = 1
tg60° = √3
tg90° = +∞

Tutto qui?
Perchè ti fermi ad un angolo di 90°?
Perchè anche la tangente, o dovrei dire la funzione tangente, gode della periodicità di seno e coseno.
Anche se è un po’ diversa.

Se usi un foglio di calcolo per fare il grafico della tangente trovi una cosa di questo tipo:

Ho preso questa immagine da un sito di matematici (youmath.it) e come vedi indicano gli angoli in radianti.
Non cambia niente e la cosa interessante è vedere che la funzione tangente si ripete sì, ma con un periodo di 180° (π), che è la metà di quello con cui si ripetono seno e coseno.

Lo puoi vedere anche dalla tabella colorata di poco fa: dopo 180° i valori della tangente si ripetono.

Il grafico della tangente non ha più niente a che vedere con la sinusoide di seno e coseno e si chiama tangentoide (e credo che tu ne abbia sentito parlare poche volte in questi termini…).

TANGENTE E PENDENZA

Dopo tutte ‘ste menate di angoli, infinito, rapporti, eccetera, arrivo a qualcosa di più concreto.

La tangente ti dice quanto è pendente un segmento o una retta.
Se α è l’angolo che forma con l’orizzontale, la tangente di α è proprio la pendenza del segmento o della retta.

È così, e se ci pensi è piuttosto potente visto che la pendenza te la ritrovi in un sacco di applicazioni tecniche.
E non solo.

Se chiamo p la pendenza di AB:

p = tgα

Ora brucerò qualche tappa ma voglio dirti ancora qualcosa sulla pendenza.

Se prendo il punto B e lo proietto sulla semiretta orizzontale che parte da A trovo C.
Il triangolo ABC è rettangolo e l’angolo retto è in C.

In un triangolo rettangolo, un cateto è uguale all’altro cateto per la tangente dell’angolo che gli è opposto.
Questo è uno degli enunciati che permettono di risolvere i triangoli rettangoli e ne scriverò in un altro post.
Qui l’ho solo anticipato.

Quindi:

BC = AC · tgα

tgα = BC / AC

Se BC è l’altezza h e AC è la base o distanza d,
allora p = h / d

Questo è utile quando devi sapere la pendenza tra due punti ma non conosci l’angolo del segmento che li unisce.

Se sei un escursionista e stai consultando una mappa per sapere qual è la via migliore per raggiungere la meta, valutare la pendenza può essere importante per evitare di camminare sulle tracce dei camosci.

Il punto A sta su una curva di livello di cui conosci la quota, Z_A, e lo stesso vale per B (la sua quota è Z_B).
Se la tua mappa è in scala (e mi auguro che lo sia!), puoi misurare la distanza planimetrica tra A e B (sulla mappa) e riportarla alla distanza reale (sempre planimetrica), d.
La pendenza del segmento che unisce A con B è presto fatta:

p_AB = (Z_B – Z_A) / d

Se il valore è troppo spinto è meglio cambiare percorso.
Potrebbe essere faticoso ed anche pericoloso!

PENDENZA E PERCENTUALE

Se sei un appassionato di ciclismo avrai familiarità con le pendenze delle grandi salite del Giro d’Italia o del Tour de France (o magari anche solo di quelle dove pedali abitualmente).
La salita dello Zoncolan, ad esempio, ha una pendenza media del 12% con punte del 22%.

Ti sarà capitato di viaggiare in auto e di imbatterti in cartelli come quello che vedi qui sotto.
Ti dice di fare attenzione perchè la strada che stai per fare ha una pendenza del 10%.

Ma che cosa c’azzecca la pendenza con la percentuale?

Questo è un modo per rendere più comprensibile qualcosa di concreto (una strada), senza usare tangenti e numeri decimali, obiettivamente poco intuitivi
Ed è anche un ottimo modo per farti sapere se devi girare la bicicletta e tornare indietro oppure sei hai le gambe buone per arrivare in cima…

Per trovare la pendenza in percentuale basta moltiplicare il valore della tagente dell’angolo per 100.
E così l’angolo 5.71059313 (espresso in gradi decimali), ha una tangente che misura 0.1 e corrisponde ad una pendenza del 10%.
Se lo guardi nei termini di differenza di altezza rispetto ad una distanza planimetrica è come dire che sei salito di 1 m per ogni 10 m percorsi in piano.

Se l’angolo è 0, anche la pendenza in percentuale è 0%.

Un angolo di 45°, che ha una tangente uguale a 1, individua una pendenza del 100%.

Se aumentano i gradi, aumentano le pendenze percentuali, ma in modo non lineare (ad 80° corrisponde una pendenza del 567%, una pendenza del 1000% corrisponde ad un angolo di 84.3°), fino ad arrivare ai 90° a cui non si attribuisce nessuna pendenza percentuale.
Perchè?
Beh, perchè non esiste la tangente di 90° e non si può dire che un muro abbia pendenza infinita.

In questo caso si abbandona la pendenza e la matematica e si usano le parole: il muro è verticale.

Se conosco la pendenza posso risalire alla misura dell’angolo con la formula inversa della tangente.
Ma questo è un altro argomento!
🙂

INFORMAZIONI DI SERVIZIO

Puoi iscriverti al canale Telegram di 3DMetrica che trovi cercando tredimetrica (telegram.me/tredimetrica) o direttamente a questo link.

Puoi ascoltare le puntate del Podcast di 3DMetrica andando alla pagina PODCASTdi questo blog.

Puoi aggiungere la tua email alla Newsletter di 3DMetrica dove, una volta alla settimana, riassumo i post che pubblico sui canali social network, linko l’ultimo articolo del blog, la nuova puntata del podcast e l’ultimo video tutorial.
Usa il box che trovi a destra e nella home page e che dice: “Iscriviti alla Newsletter“.

Ed infine c’è anche il canale You Tube in cui carico video tutorial sull’uso di specifici software per la fotogrammetria e la gestione dei dati tridimensionali.

Se questo articolo ti è stato utile puoi scegliere di supportare la creazione e la condivisione di cotenuti simili diventando un finanziatore di 3DMetrica su Patreon.
Puoi unirti a chi ha già scelto di aiutarmi a rendere il progetto possibile e sostenibile.
Trovi tutte le informazioni e puoi scoprire come fare a questo link.