Dopo averti scritto di seno e coseno e della tangente di un angolo ti devo dire ancora alcune cose sulle funzioni goniometriche.
Non saranno molte, ma mi servono per concludere questo breve viaggio nella trigonometria, necessario per affrontare quello, ben più lungo, nella misura topografica.
In questo articolo ti parlo dei reciproci e degli inversi delle funzioni goniometriche.
IL RECIPROCO DI SENO, COSENO E TANGENTE
Non vorrei farmi dei nemici ma non è che ci sia molto da dire sul reciproco di qualcosa…
Si tratta di fare “1 diviso quel qualcosa“.
In trigonometria i reciproci delle funzioni goniometriche devono avere ammaliato qualcuno di quelli che hanno “scritto le regole” perchè gli hanno dato dei nomi propri.
Il reciproco di una funzione è quella funziona che viene fuori dividendo 1 per la funzione di cui vuoi fare il reciproco.
Sembra uno scioglilingua ed un po’ lo è, quindi te lo scrivo chiaro e in breve:
1/x è il reciproco di x;
1/f(x) è la funzione reciproca di f(x).
Tutto qui…
Ah no, in trigonometria ci sono anche i nomi.
Il reciproco della funzione seno si chiama cosecante.
Il reciproco della funzione coseno si chiama secante.
Il reciproco della funzione tangente si chiama cotangente.
Nota personale: se cambiavano il nome di secante e cosecante creavano meno confusione.
🙂
Comunque:
cosecα = 1/senα
secα = 1/coseα
cotgα = 1/tgα
Siccome
tgα = senα / cosα
allora
cotgα = cosα / senα
ma anche
cotgα = cosecα / secα
Una cosa da dire sulle funzioni reciproche però c’è: secante e cosecante non esistono sempre.
Sì perchè seno e coseno possono essere anche 0.
Il seno di 180°, per esempio, è 0.
Così come lo è il coseno di 90°.
Ecco, per questi angoli, le funzioni secante e cosecante si comportano proprio come la tangente di 90°.
1/0 = ∞
Questo significa che non esiste un valore finito di secante e cosecante per questi angoli (che sono 0° e 180° per la cosecante e 90° e 270° per la secante ed i rispettiVI angoli che si ottengono aggiungendo 180°) ma prende un valore “infinito“.
Come le funzioni madri, anche i reciproci sono periodici.
I loro valori si ripetono con lo stesso periodo dei loro “genitori”: 360° per secante e cosecante e 180° per la cotangente.
Delle funzioni reciproche ci sono i grafici e tra le pagine dei libri di matematica trovi anche qualcosa in più, ma io mi fermo qui.


FUNZIONI INVERSE: ARCOSENO, ARCOCOSENO E ARCOTANGENTE
Una funzione goniometrica ti dice il valore del seno, coseno o della tangente di un angolo.
Ma ci sono anche le funzioni inverse, quelle che ti sanno dire qual è l’angolo il cui seno, coseno o tangente è un certo numero.
Ad esempio, se ti chiedo qual è l’angolo la cui tangente è 1, la risposta è 45°.
E qual è l’angolo il cui seno è 0.5?
30°.
Ecco, per fare questo hai applicato l’inverso delle due funzioni goniometriche.
Dai si trattava di casi semplici.
Ma se ti chiedo l’angolo il cui coseno è 0.729 le cose non sono così immediate.
L’inverso della funzione seno è l’arcoseno, arcsen.
L’inverso del coseno è l’arcocoseno, arcos.
E per la tangente c’è l’arcotangente, arctg.
Nelle calcolatrici ed in giro per i pc potresti trovarli indicati così:
sen-1
cos-1
tg-1
Non devi diventare pazzo o pazza per leggere ed imparare algoritmi per il calcolo delle funzioni inverse, a supportarci ci sono proprio le calcolatrici ed anche i fogli di calcolo.
Ci pensano loro!
Ma c’è un problema con le funzioni inverse.
Ed è legato alla periodicità delle funzioni goniometriche principali.
IL PROBLEMA DELLE FUNZIONI INVERSE
Se è vero che per ogni angolo esiste un solo valore di seno, un solo coseno ed una sola tangente, è anche vero che ci sono angoli che hanno lo stesso seno, coseno e tangente (α+360°; α+720°, …)
E quindi per ogni numero (all’interno del campo dei risultati delle funzioni goniometriche) ci sono più angoli il cui seno, coseno o tangente sono proprio quel numero.
E questi angoli sono infiniti.

Si vede piuttosto bene dal grafico della funzione seno, che si ripete ogni 360°.
Se tracci una linea orizzontale che interseca la sinusoide, ti accorgi che la taglia un sacco di volte, trovando altrettanti angoli.
Di questi solo due stanno dentro il primo giro del cerchio goniometrico (cioè sono minori – o uguali – di 360°).
Questo è un problema in matematica ed in topografia perchè mette in crisi il concetto tanto caro di univocamente determinato, riportando in scena, prepotentemente, l’ambiguità legata agli angoli.
Ed allora la soluzione sta nel restringere il campo di validità delle funzioni inverse.
Quelli bravi lo chiamano “dominio“.
Ecco come.
ARCOSENO

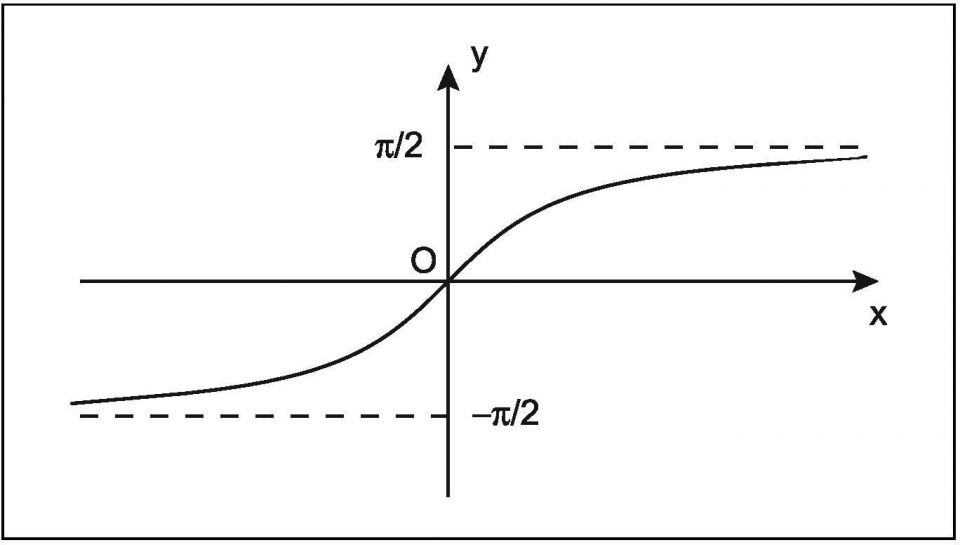
Per eliminare l’ambiguità dell’inverso della funzione seno, l’arcoseno, la devi considerare valida solo per gli angoli che vanno da -90° a 90°.
In questo intervallo ad ogni numero (compreso tra -1 e 1) corrisponde un solo angolo.
Ecco il grafico della funzione arcoseno.

ARCOCOSENO
Per l’arcocoseno, l’inverso del coseno, le cose sono simili all’arcoseno ma il dominio di validità è diverso.

L’arcocoseno infatti vale per angoli compresi tra 0° e 180°.
Ecco il suo grafico:

ARCOTANGENTE
Ed infine c’è l’arcotangente, l’inverso della tangente, che vale, come l’arcoseno, tra -90° e 90°.

FUNZIONI INVERSE vs INVERSO DELLE FUNZIONI
Non c’è molto altro da dire in questo capitolo, forse un po’ grigio di contenuti.
Chiudo con una considerazione/raccomandazione.
C’è un’enorme differenza tra funzione inversa ed inverso della funzione.
L’inverso della funzione l’ho chiamato reciproco, agganciandomi all’aritmetica pura ed al reciproco dei numeri.
La funzione inversa è tutta un’altra storia.
Attenzione a non confonderli tra loro!
🙂
INFORMAZIONI DI SERVIZIO
Puoi iscriverti al canale Telegram di 3DMetrica che trovi cercando tredimetrica (telegram.me/tredimetrica) o direttamente a questo link.
Puoi ascoltare le puntate del Podcast di 3DMetrica andando alla pagina PODCASTdi questo blog.
Puoi aggiungere la tua email alla Newsletter di 3DMetrica dove, una volta alla settimana, riassumo i post che pubblico sui canali social network, linko l’ultimo articolo del blog, la nuova puntata del podcast e l’ultimo video tutorial.
Usa il box che trovi a destra e nella home page e che dice: “Iscriviti alla Newsletter“.
Ed infine c’è anche il canale You Tube in cui carico video tutorial sull’uso di specifici software per la fotogrammetria e la gestione dei dati tridimensionali.
Se questo articolo ti è stato utile puoi scegliere di supportare la creazione e la condivisione di cotenuti simili diventando un finanziatore di 3DMetrica su Patreon.
Puoi unirti a chi ha già scelto di aiutarmi a rendere il progetto possibile e sostenibile.
Trovi tutte le informazioni e puoi scoprire come fare a questo link.








Lasciami un commento!
Leave A Reply